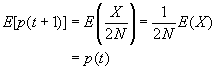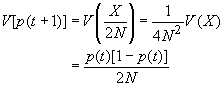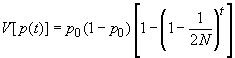C/ MODELISATION MATHEMATIQUE

 

 

                                               1 Le modèle de Wright-Fischer est basé sur une loi binomiale (17)(8)

 

Comme nous l'avons vu  précédemment avec la notion d'urne gamétique (cf grand B petit 2) produire une nouvelle génération t+1 consiste à répéter 2N expèriences élémentaires de probabilité p de tirer un allèle A .On définit par q la probabilité de tirer l'allèle a.

 

ainsi : p+q = 1 donc q = 1 – p

 

Chaque tirage se fait avec remise (cf grand B petit 2 ) .Il est donc indépendant et ne peut avoir que deux issues contraires A (probabilité p) et a (probabilité 1-p)

Nous sommes donc dans le cas de figure d'une épreuve de Bernouilli de paramètre p (6)

Ainsi pour la variable aléatoire x qui associe 1 au tirage de l'allèle A et 0 au tirage de l'allèle a on peut définir la loi de probabilité par :

 

        valeurs r prises par x :     ( 0  )          (  1 )

                                                 

        Probablité p(X = r)      :   ( 1 - p )        (  p )

 

 

L'esperance sera donc E(x) = p et la variance V(x) = p (1 – p) (6)

 

Notre nouvelle génération est donc la répétition de 2N épreuves de Bernouilli de paramètre p

La variable aléatoire X correspondra alors au nombre de succès r soit le nombre d'allèle A à la prochaine génération:chiffre donc compris entre 0 et 2N

On peut donc dire que X suit une loi binomiale de paramètre 2N et p notée B( 2N, p )

La probabilité d'observer r allèles A est donnée par :

 

 

 

 

et r peut donc varier de 0 à 2N copies, impliquant que p(t+1) peut prendre des valeurs variant entre et comprenant 0 et 1, avec une certaine probabilité donnée par la loi binomiale. 

 

L'espérance de X est bien sûr donné par E(X) = 2N p  (*), et sa variance par V(X) = 2N p (1-p) (**) soit 2N fois l'espérance et la variance de la loi de bernouilli (6)

On peut facilement obtenir l'espérance et la variance de p(t+1):

                           puisque p est la fréquence allèlique de A, p(t+1) est la fréquence de A à t+1 donc  égale au nombre d'allèle A tirés parmis les 2N allèles on peut écrire   p(t+1) = X/2N   et son espérance :

 

E(p(t+1)) = E(X/2N) = E(X)/2N or comme déjà vu ci-dessus(*) E(X) = 2Np(t)

 

donc on peut écrire E(p(t+1)) = E(X) / 2N = 2Np(t) / 2N = p(t)

 

On retrouve la formule de l'espérance

 

 

 

 

 

De même pour la variance p(t+1) = X/2N et V(X) = 2N p (t)(1-p(t)).(**)

V(p(t+1)) = V(X/2N) = V(X) / 4N2 = 2N p (t)(1-p(t)) / 4N2 = p (t)(1-p(t)) / 2N

On retrouve la formule de la VARIANCE

 

 

 

 

 

 

 

"Ces différentes courbes correspondent à des réplications indépendantes du processus d'évolution des fréquences alléliques à partir d'une même fréquence initiale. Cela pourrait correspondre à l'évolution de différents locus dans la même population, ou à l'évolution de différentes populations ayant divergé à partir d'une certaine population ancestrale. Dans ce cas, on se rend compte que la divergence des populations augmente régulièrement au cours du temps.cette divergence est liée à l'augmentation de la variance des fréquences allélique de génération en génération. On peut en effet montrer que l'évolution de la variance au cours du temps est donnée par" (17)(8)

 

 

 

 

 

 

si t augmente 1-1/2N étant toujours inférieur à 1 diminue ,donc 1-( 1-1/2N)t augmente

p0(1-p0) multiplié par un facteur qui augmente augmente également

donc V(p(t)) augmente bien quand t augmente

 

 

                                                                2 Notion d'effet d'échantillonage

 

L'espèrance de la fréquence de l'allèle A à la génération t+1 est égale a la fréquence à la génératon t .Ce qui signifie qu'elle est constante.L'esperance correspond à la moyenne empirique pris par la variable aléatoire (ici la fréquence de l'allèle A ) au bout d'un grand nombre d'experiences .Ce qui permet de comprendre notre observation de la page 6 (commentaire de la dernière courbe« En observant les courbes des differentes évolutions simulées on constate que la moyenne des fréquences allèliques tend vers la fréquence initiale de 0,5. »).Ainsi on comprend pourquoi en multipliant les essais d'évolution de population on tend vers la fréquence initiale.En fait on rejoint alors les prévisions du modèle de Hardy-Weinberg puisque en multipliant les expèriences on tend vers une infinité de simulations de petites populations ce qui statistiquement correspond alors à l'hypothèse de population infinie de Hardy-Weinberg

 

la variance ,par contre est inversement proportionnelle à N .Donc plus la population sera petite plus la variance augmentera .La variance mesure la dispersion de la variable aléatoire mesurée , ainsi plus la variance de la variable « fréquence allèlique de A » augmente plus la fréquence aux génerations suivantes sera dispersée(cf livre math 1er S belin p256) .La variance est le fondement mathématique des propri étés de la dérive génétique :

 

                                 -V (frequence allèlique)  est inversement proportionnelle à la taille de la population ce qui explique cette propriété de la dérive génétique .

 

                                 -V (fréquence allèlique)  est un paramètre de dispertion qui augmente avec V(X) (7) d'ou le caractère imprévisible (stochastique ) des tirages aléatoires ce qui explique la notion d'effet d'échantillonnage .L'effet d'échantillonnage est le phénomène purement aléatoire qui est le moteur de la dérive génétique .

 

                  Par exemple tiront 10 allèles avec remise dans une urne gamétique, comprenant 5 allèles A et 5 allèles a .Il est aisé de comprendre qu'il assez probable d'avoir des résultats differents de la moyenne 5A /5a : par exemple 6A/4a ou même 3A/7a , le tirage de la génération suivante engendrera également des résultats éloignant encore plus de 5A/5a etc...c'est la définition de la dérive génétique

Par contre si nous tirons 100000 allèles avec remise dans une urne contenant 50000 A et 50000 a ,les résultat se rapprocherons beaucoup plus des proportions d'origines par exemple 51000 A 49000 a

En augmentant N nous baissons la variance donc limitons l'effet d'échantillonage et nous nous rappochons du modèle de population infinie de Hardy-Weinberg (7)

 

                                                                         CONCLUSION

 

 

Le modèle de Wright-Fischer ainsi que sa simulation informatique nous ont permis de mettre en évidence une divergence génétique des populations: la dérive génétique  .Son étude mathématique nous a permis de déterminer et de comprendre ses principales propriétés : la dérive génétique est :

 

                  - Un phénomène purement aléatoire (stochastique ) lié à un effet d'échantillonage marqué (lié à une variance élevée)

 

                  - d'autant plus forte que la taille de la population est faible ( variance inversement proprtionnelle à N)

 

Grace aux simulations nous avons également pu découvrir les conséquences des effets de la dérive génétique .Elle entraine inévitablement une fixation allèlique . La dispariton des allèles non fixées aboutit à une baisse de la diversité génétique de l'espèce touchée par la dérive .

Puisqu'elle modifie les fréquences allèliques ,la dérive génétique est donc une force évolutive qui agit fortement sur les espèces aux effectifs réduits .Elle serait donc au sens strict bien un « moteur » pour l'évolution (3)

 

Cependant elle provoque un affaiblisement par perte de diversité génétique et ce d'autant plus rapidement que l'espèce est en nombre réduit . Si cette appauvrissement génétique d'une espèce aux effectifs déjà laminés par des catastrophes environnementales (chasse,pollution...) entrainait l'exctinction nous serions dans un cas de figure paradoxal où une force (« moteur ») évolutive serait responsable de la fin de l'évolution d'une espèce puisque cause de son extinction. .Elle constiturait ,alors en quelque sorte , un « frein » à son évolution.

 

Le modéle de Wright-Fischer est  une simplification théorique puisqu'il exclut les autres forces évolutives (mutation, selection et migrations ) et limite la population à un effectif constant .Il faut en tenir compte avant de conclure de façon trop tranchée .La réalité est infiniment plus complexe et source de surprises .

Pour explorer les implications de notre problématique nous devons tenter de répondre à la question suivante :

Une espèce menacée (d'effectif donc déjà faible) subissant fortement une dérive génétique est elle condamnée  à l'extinction ? (11)

Pour y répondre nous essayerons dans une deuxième partie d'inscrire la dérive génétique dans une histoire plus réaliste de l'espèce menacée en prenant en compte plus de paramètres : ceux à l'origine de la chute des effectifs (effet « bottelneck ») ,ceux menacant son avenir (notion de consanguinité et de spirale d'extinction)

Pour ce faire nous nous aiderons d'exemples concrets .